DFG-SPP 1324
Mathematical methods for extracting quantifiable information from complex systems
This program was approved by the Senate of the DFG on April the 27th, 2007 (Press release).
Abstract
Mathematical models of complex systems form the foundation for further technological developments in science, engineering and computational finance; particularly important but also particularly challenging problems arise in connection with high-dimensional parameter spaces. Motivated by the continuously increasing computer power ever more realistic models have been developed in recent years. These models have also become increasingly complex, and their numerical treatment is facing serious challenges.
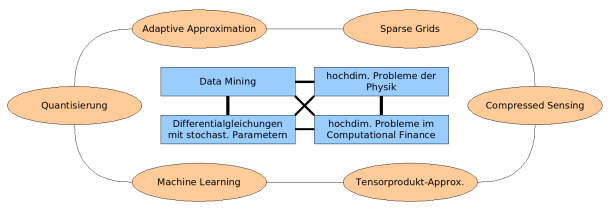
To overcome these difficulties, a possible approach would be to start with the application at hand and to concentrate on this particular case. However, within this Priority Programme, we propose a different strategy. Recent developments in mathematics suggest that in the long run, much more powerful solution strategies can be derived if the interconnections between the different fields of research are systematically exploited at a conceptual level. In order to do so, a deeper understanding of the mathematical foundations as well as the development of new and efficient numerical algorithms will be the main goals of this Priority Programme.
The treatment of high-dimensional systems is clearly one of the most challenging tasks in applied mathematics. Since the problem of high-dimensionality appears in many fields of applications, the above mentioned synergy and cross-fertilisation effects are very likely to make a great impact. To be really successful, the following issues have to be kept in mind: theoretical research and practical applications must be developed hand in hand; moreover, it is necessary to combine different fields of mathematics, such as numerical analysis and stochastics. To keep the whole programme sufficiently focussed, we will concentrate on specific, but related fields of applications such as data mining, high-dimensional problems in physics, computational finance and differential equations with random coefficients. All these applications share common characteristics and, therefore, they allow for closely related approaches.


